蓝桥杯C常用算法

精度处理

例如：我们想要程序判别 0.1+0.2 == 0.3

1.比较法

取等式差值的绝对值小于某一个特别小的数，若差值小于特别小的数则条件成立，反之。

1
2
3
4
if( fabs(0.2 + 0.1 - 0.3) <= 1E-10 ) // 一般1的负10次方够用了
        cout << "true" << endl;     
    else 
        cout << "false" << endl;

2.整型比较

由于计算机对于整形的运算绝对精准，所以把浮点运算化整形运算的做法是我们常用的。 将等式两边分别乘以10

1
2
3
4
if(1 + 2 == 3)
        cout << "true" << endl;     
    else 
        cout << "false" << endl;

最大公约数&最小公倍数

最大公约数

1.短除法

1
2
3
4
5
6
7
/**短除法*/
int enum_max_common_divisor(int a, int b)// 大的值为b，枚举法 
{
    for(int i = a; i >= 1; i--)   // 当两个数互质时，则最大公约数为I 
        if(a % i == 0 && b % i == 0)        
            return i;   
}

2.辗转相除法

1
2
3
4
5
6
/**辗转相除法*/ 
int max_common_divisor(int a, int b)// 递归辗转除法,优点：a,b可以任意值输入 
{ 
    if(a == 0) return b;
     return max_common_divisor(b % a, a);
}

最小公倍数

最小公倍数 = a*b /最大公约数

1
2
3
4
5
6
/*最小公倍数= a*b /最大公约数 
  a= ka*i  b= kb*i    a*b = ka*kb*i*i    */ 
int min_common_multiple(int a, int b)
{
    return a * b / max_common_divisor(a, b);
}

递归

递归的特点：

  1. 递归就是方法里调用自身。

  2. 在使用递增归策略时，必须有一个明确的递归结束条件，称为递归出口。

  3. 递归算法解题通常显得很简洁，但递归算法解题的运行效率较低。所以一般不提倡用递归算法设计程序。

  4. 在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储。递归次数过多容易造成栈溢出等，所以一般不提倡用递归算法设计程序。

    构造递归主要是构造出口(output)和移动变量(moveParameter)。

例子 1.斐波纳契数列（Fibonacci Sequence） 在数学上，斐波纳契数列以如下被以递归的方法定义：F1=1,F2=1,Fn=F（n-1）+F（n-2）（n>2,n∈N*））

1
2
3
4
5
6
7
8
9
10
11
int fib(int index)
{
       if (index == 1 || index == 2)// 出口
   {  
          return 1;  
    }
    else
    {  
          return fib(index - 1) + fib(index - 2);  
    }
}

2.N的阶层

1
2
3
4
5
6
7
8
9
10
11
int factorial(int index)
{
    if(index == 1)
    {  
            return 1;  
    }
    else
    {  
            return factorial(index - 1) * index;  
    } 
}

递归算法转换成为非递归算法

将递归算法转换为非递归算法有两种方法，一种是直接求值，不需要回溯；另一种是不能直接求值，需要回溯。前者使用一些变量保存中间结果，称为直接转换法；后者使用栈保存中间结果，称为间接转换法，下面主要介绍直接转换法。 直接转换法通常用来消除尾递归和单向递归，将递归结构用循环结构来替代。尾递归是指在递归算法中，递归调用语句只有一个，而且是处在算法的最后。例如求阶乘的递归算法：

1
2
3
4
5
6
7
long fact(int n)
　　{
   　　if (n == 0) 
       　　return 1;
   　　else 
       　　return n * fact(n - 1);
　　}

当递归调用返回时，是返回到上一层递归调用的下一条语句，而这个返回位置正好是算法的结束处，所以，不必利用栈来保存返回信息。对于尾递归形式的递归算法，可以利用循环结构来替代。例如求阶乘的递归算法可以写成如下循环结构的非递归算法：

1
2
3
4
5
6
7
long fact(int n)
{
    　　int s = 1;
    　　for (int i = 1; i < n; i++)
        　　s = s * i; // 用s保存中间结果
    　　return s;
　　}

单向递归是指递归算法中虽然有多处递归调用语句，但各递归调用语句的参数之间没有关系，并且这些递归调用语句都处在递归算法的最后。显然，尾递归是单向递归的特例。例如求斐波那契数列的递归算法如下：

1
2
3
4
5
6
7
int f(int n)
　{
    　　if (n ==1 || n == 0) 
    　　return 1;
    　　else 
    　　return f(n - 1) + f( n-2 );
　　}

对于单向递归，可以设置一些变量保存中间结构，将递归结构用循环结构来替代。例如求斐波那契数列的算 法中用s1和s2保存中间的计算结果，非递归函数如下：

1
2
3
4
5
6
7
8
9
10
int f(int n)
{
　　int a[n + 2];
    a[1] = 1, a[2] = 1;
　　for(i=3;i <= n; i++)
    {
        a[i] = a[i - 1] + a[i - 2]; 
    }
　　return a[n];
}

递归经典竞赛应用

李白打酒

1
2
3
4
5
6
7
8
9
话说大诗人李白，一生好饮。幸好他从不开车。

一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：

逢店加一倍，遇花喝一斗。

这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。

请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int total = 0;  
int a(int s, int f, int d)
{  
    if(s > 0) // 当店大于0，就行搜索   
        a(s - 1, f, d * 2); // return a(s-1,f,d*2); 
    if(f > 1) // 花大于1，进行搜索   
        a(s, f - 1, d - 1);  

    if(s == 0 && f == 1 && d == 1) // 保证最后一次遇见的是花 此时还剩下1斗酒   
        total++;  

    return total;  
}  
int main()
{  
    printf("%d", a(5, 10, 2)); // 初始化为最初有 5个店 10个花 2斗酒   
    return 0;  
}

第39级台阶

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm> 

#define LEFT false
#define RIGHT true

using namespace std;

static int total;
void f(int step, bool flag)
{
    if(step > 39)// 出口
        return ;
if(flag == RIGHT && step == 39)// 判断条件是否符合
{
    total++;
    return;
}
f(step + 1, !flag);// 遍历迈一步的方式
f(step + 2, !flag);// 遍历迈两步的方式
}

int main()
{
    f(1, LEFT); //第一步迈一步 
    f(2, LEFT);//第一步迈两步 
    cout << total;
    return 0;
}

返回累加性解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#define LEFT false
#define RIGHT true

static int total;

long f(int step, bool flag)
{
     if(step == 1)// 判断第一步左脚是一步
     {  
         if(flag == RIGHT)  
            return 1;  
         else 
            return 0;  
     }  
     else if(step == 2)// 判断第一步左脚是两步，必定最后一步为右脚
     {  
        return 1;  
     }  
if(flag == RIGHT && step == 0)
{
    return 1;
}
else if(step <= 0)
{
    return 0;
}

return f2(step - 1, !flag) + f2(step -2, !flag);
}

int main()
{
    cout<<f(39,LEFT)<<endl;
    cout<<total;
    return 0;
}

DFS

回溯型DFS

字符串全排列

DFS构建步骤

  1. 设定step出口变量，在出口处拦截适宜的数据；
  2. 构造原数据数组old && 移动数据数组a[]；
  3. for循环处对数据进行排列置换
  4. for循环步骤 ：判断使用标志位i下标的数据为未被使用，条件成立->置该数组下标使用标志->置换数据a[step] = old[i]，注意前者是出口移动变量，后者是i变量->递归dfs(step+1),使函数步移->回溯，置该标志位数组下标未使用标志
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#define ARRAY_LENGTH 4
#define NOT_USED 0
#define USED 1

char old[ARRAY_LENGTH] = {'a', 'b', 'c', 'd'};
char a[ARRAY_LENGTH];
int useFlag[ARRAY_LENGTH];

void dfs(int step)
{
    if(step >= ARRAY_LENGTH)    // 出口，过滤数据找出结果 
    {
        for(int i = 0; i < ARRAY_LENGTH; i++)
        {
            cout << a[i] << " ";
        }
        cout << endl;
        return ;
    }
    for(int i = 0; i < ARRAY_LENGTH; i++)
    {
        if( useFlag[i] == NOT_USED) // 判断该下标的标志位是否被使用 
        {
            useFlag[i] = USED;      // 置使用标志 
            a[step] = old[i];       // 置换数据，排列数组 
            dfs(step + 1);            // 递归    
            useFlag[i] = NOT_USED; // 回溯 
        }
    }
}

int main(void)
{   
    memset(useFlag, NOT_USED, sizeof(useFlag));
    dfs(0);     
    return 0;
}

从for循环角度理解不回溯型DFS

1
2
3
4
小明与其他3人玩牌。
一副扑克牌（去掉大小王牌，共52张），均匀发给4个人，每个人13张。
这时，小明脑子里突然冒出一个问题：
如果不考虑花色，只考虑点数，也不考虑自己得到的牌的先后顺序，自己手里能拿到的初始牌型组合一共有多少种呢？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int main()
{
    int sum = 0;
    int total = 0;
    int a[14];
    for (a[1] = 0; a[1] <= 4; a[1]++)                                                    //1
        for (a[2] = 0; a[2] <= 4; a[2]++)                                                //2
            for (a[3] = 0; a[3] <= 4; a[3]++)                                            //3
                for (a[4] = 0; a[4] <= 4; a[4]++)                                        //4
                    for (a[5] = 0; a[5] <= 4; a[5]++)                                    //5
                        for (a[6] = 0; a[6] <= 4; a[6]++)                                //6
                            for (a[7] = 0; a[7] <= 4; a[7]++)                            //7
                                for (a[8] = 0; a[8] <= 4; a[8]++)                        //8
                                    for (a[9] = 0; a[9] <= 4; a[9]++)                    //9
                                        for (a[10] = 0; a[10] <= 4; a[10]++)             //10
                                            for (a[11] = 0; a[11] <= 4; a[11]++)         //11
                                                for (a[12] = 0; a[12] <= 4; a[12]++)     //12
                                                    for (a[13] = 0; a[13] <= 4; a[13]++) //13
                                                    {
                                                        for (int i = 1; i <= 13; i++)
                                                        {
                                                            sum += a[i];
                                                        }
                                                        if (sum == 13)
                                                        {
                                                            total++;
                                                        }
                                                        sum = 0;
                                                    }

    cout << total;

    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
parameter： n:步移 ； cartNum:手上的牌数量 ； 这两个变量为控制出口变量。  
*/ 
void dfs(int n, int cartNum)  
{

    if(n > 14)        // 出口1：抽牌的次数(13次)越界 相当于for循环阶数:13阶 
    {
        return;
    }

    if (cartNum >= 13)     // 出口2：牌数量越界 
    {
        if (cartNum == 13) // 截取条件成立的结果 
            sum++;
        return;
    } 
    else            // 相当于for循环中的条件int a=0~a<=4; 
    {
        dfs(n + 1, cartNum+1);     // 有一张该类的牌  
        dfs(n + 1, cartNum+2);     // 有两张该类的牌 
        dfs(n + 1, cartNum+3);     // 有三张该类的牌 
        dfs(n + 1, cartNum+4);     // 有四张该类的牌 
    }

}

竞赛应用

带分数

1
2
3
4
5
6
7
100 可以表示为带分数的形式：100 = 3 + 69258 / 714

还可以表示为：100 = 82 + 3546 / 197

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

类似这样的带分数，100 有 11 种表示法。

题目要求： 从标准输入读入一个正整数N (N<1000*1000) 程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。 注意：不要求输出每个表示，只统计有多少表示法！

例如： 用户输入： 100 程序输出： 11

再例如： 用户输入： 105 程序输出： 6

资源约定： 峰值内存消耗 < 64M CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

**dfs N=A+B/C⇨B=(N-A)*C。根据公式，只需要求A和C就可以进行判断了。A的范围是1-N，但是这些数中有很多是无用的（如：11，101……）。我们只选有用的数，用vis数组标记1-9中已经用过的数字，避免做不必要的搜索。**

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
#include <iostream>
using namespace std;
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>

int ans = 0; //
bool vis[10];
int n;
int A = 0, C = 0;
int lenN;
int ALEN = 0, CLEN = 0;
bool judge()
{
    bool vistemp[10];
    memcpy(vistemp, vis, sizeof(vis));
    int t = (n - A) * C;
    int BLEN = 0;
    while (t)
    {
        if (vistemp[t % 10])
            return false;
        vistemp[t % 10] = 1;
        BLEN++;
        t /= 10;
    }
    return BLEN + ALEN + CLEN == 9;
}

void dfs(int flag)
{
    if (flag == 2)
    {
        if (judge())
            ans++;
        return;
    }
    for (int i = 1; i <= 9; i++)
    {
        if (vis[i])
            continue;
        vis[i] = 1;
        if (flag == 1)
        {
            A *= 10;
            A += i;
            ALEN += 1;
            if (A <= n)
            {
                dfs(1);
                dfs(3);
                ALEN -= 1;
                A /= 10;
            }
            else if (A > n)
            {
                ALEN -= 1;
                A /= 10;
                vis[i] = 0;
                break;
            }
        }
        else if (flag == 3)
        {
            if (CLEN < (9 - ALEN) / 2)
            {
                C *= 10;
                C += i;
                CLEN++;
                dfs(2);
                dfs(3);
                C /= 10;
                CLEN--;
            }
            else
            {
                vis[i] = 0;
                break;
            }
        }
        vis[i] = 0;
    }
}
int main()
{
    cin >> n;
    int temp = n;
    lenN = 0;
    while (temp)
    {
        lenN++;
        temp /= 10;
    }
    memset(vis, 0, sizeof(vis));
    vis[0] = 1;
    dfs(1);
    cout << ans << endl;
    return 0;
}

地宫取宝

1
2
3
4
5
6
7
8
9
10
11
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是k件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这k件宝贝。

【数据格式】

1
2
3
4
5
6
输入一行3个整数，用空格分开：n m k (1<=n,m<=50, 1<=k<=12)

接下来有 n 行数据，每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值

要求输出一个整数，表示正好取k个宝贝的行动方案数。
该数字可能很大，输出它对 1000000007 取模的结果。

例如，输入： 2 2 2 1 2 2 1 程序应该输出： 2

再例如，输入： 2 3 2 1 2 3 2 1 5 程序应该输出： 14

资源约定： 峰值内存消耗 < 256M CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入…” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0 注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。 注意: 所有依赖的函数必须明确地在源文件中 #include ， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

4维的记忆化DFS,题目要求只能下或右走，从左上角走到右下角，记录下每个坐标下的数量和最大宝贝价值下的走的情况

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include <stdio.h>
#include <string.h>
#include <string>
#include <algorithm>
#include <math.h>
#include <iostream>
#include <time.h>

#define mod 1000000007
using namespace std;

int n, m, k;
int c[55][55];
int dp[55][55][101][15];
int dfs(int x, int y, int mun, int v) //x,y表示坐标，mun表示手中宝贝的数量，V表示手中的最大宝贝的价值
{
    if (dp[x][y][mun][v] != -1)  //记录了经过 此坐标此数量此价值下的所有走法，
        return dp[x][y][mun][v]; //所以直接返回，后面的无需走了

    if (x == n - 1 && y == m - 1)
    {
        if (mun == k || (mun == k - 1 && c[x][y] > v)) //符合要求的算一种
            return dp[x][y][mun][v] = 1;
        else
        {
            return dp[x][y][mun][v] = 0; //不符合
        }
    }

    int t = 0;

    if (y + 1 < m))//x<n-1
        {
            if (c[x][y] > v) //选择拿起宝贝
            {
                t = (t + dfs(x, y + 1, mun + 1, c[x][y])) % mod;
            }

            t = (t + dfs(x, y + 1, mun, v)) % mod; //选择不拿
        }

    if (x + 1 < n) //x<n-1
    {
        if (c[x][y] > v)
        {
            t = (t + dfs(x + 1, y, mun + 1, c[x][y])) % mod;
        }

        t = (t + dfs(x + 1, y, mun, v)) % mod;
    }

    return dp[x][y][mun][v] = t % mod; //由右和下返回的值记录于此坐标下，下次路过此时
    //不再递归
}
int main()
{
    memset(dp, -1, sizeof(dp)); //标志
    scanf("%d%d%d", &n, &m, &k);

    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
        {
            scanf("%d", &c[i][j]);
            c[i][j]++; //为什么加1,因为有的宝贝价值问0，会出现比较错误
        }

    printf("%d\n", dfs(0, 0, 0, 0));
    return 0;
}

贪心算法与分治策略

贪心算法

严格来说，贪心算法并不是某些有明确指向的算法，而是代指一类算法思想。在有多种决策可选时，我们会选择一个最优的策略，即所谓的贪心算法。

举一个简单的例子，田忌赛马。在对方出上等马时，我们没有任何一匹马能赢这一局，既然注定时输，那么我们希望尽量减少我们的损失。何为损失？我们每一局都会用掉一匹马，那么对于必输的局，显然用掉最弱的马是最好的。这里就可以归类出两个名词：

  1. 局部目标：在贪心问题中，总归有一个局部的目标。例如在上述场景里，我们希望减少这一轮的损失。这就是一个局部目标。和局部目标对应的是全局目标，全局上来说我们当然希望最终能赢得比赛。
  2. 策略：在这个局部场景中，我们可以有多种可用的决策，例如我们可以挑选任意一匹马应战。

实际上，很多问题都可以拆解为若干个局部问题和局部策略。如果这一类问题满足：

  1. 局部问题存在最优解。
  2. 局部问题最优可以保证全局问题最优。

那么这个问题就可以通过贪心算法解决。

小技巧：局部问题又称为子问题，很多复杂的原始问题都可以拆解成若干个子问题构成，例如一盘围棋就可以拆解为每次双方执子的小问题。在不同的情景下，子问题的性质是不一样的，对应的解决办法也不一样。例如：

  • 子问题最优则原始问题最优——贪心算法或者动态规划算法。
  • 子问题最优则原始问题最优，且子问题互相独立——分治算法。
  • 子问题最优不能推导出原始问题最优——暴力搜索等。

简单来说，** 贪心算法采用贪心的策略，保证每次操作都是局部最优的，从而使最后得到的一个结果是_全局最优_的。**

贪心算法举例：

问题：

有一群孩子和一堆饼干，每个孩子有一个饥饿度，每个饼干都有一个大小。每个孩子只能吃最多一个饼干，且只有饼干的大小大于孩子的饥饿度时，这个孩子才能吃饱。求解最多有多少孩子可以吃饱。

输入输出样例：

输入两个数组，分别代表孩子的饥饿度和饼干的大小。输出最多有多少孩子可以吃饱的数量。

1
2
Input：[1, 2], [1, 2, 3]
Output：2

** 题解：**

原始问题可以划分为给每个孩子分配饼干，即子问题。这里子问题的最优解就是用最小的饼干满足当前孩子。

** 代码：**

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int findContentChildren(vector<int>& g, vector<int>& s) 
    {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());

        int l_g = g.size();
        int l_s = s.size();
        int child = 0, cookie = 0;

        while (child < l_g && cookie < l_s)
        {
            if (g[child] <= s[cookie])
            {
                child++;
                cookie++;
            } else{
                cookie++;
            }
        }
        return child;
    }

分治策略

复杂的原始问题可能可以拆分成若干个子问题，如果子问题之间互相独立（一个子问题的计算结果不依赖于其他子问题），那么原始问题可以被分治法解决。

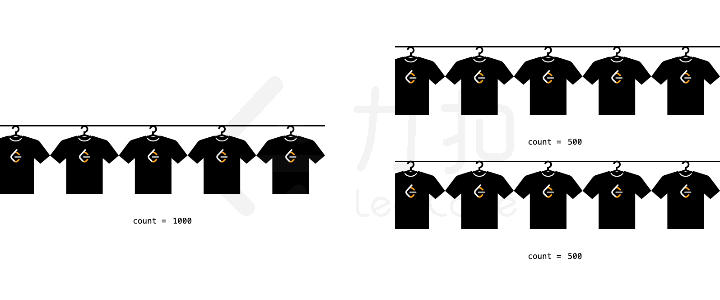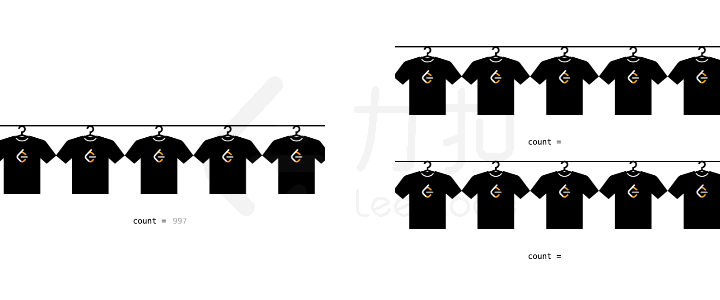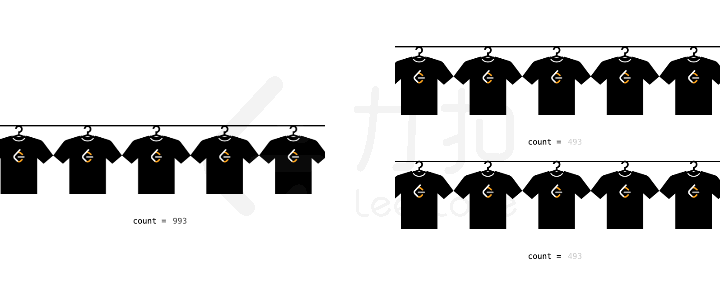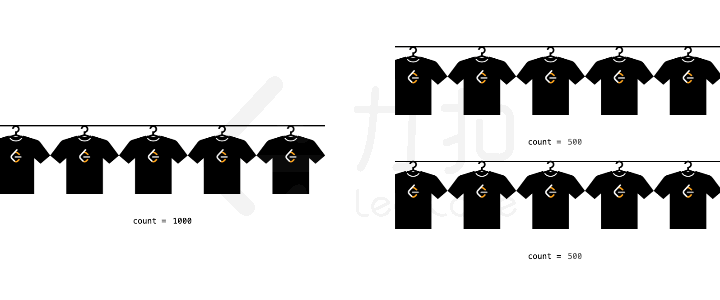
单提概念不太容易理解，我们考虑一个具体的场景。假设我们要生产 1000 件衣服，每条流水线每分钟可以生产 1 件衣服。那么如果我们有两条流水线，就可以把原始问题拆解为两个生产 500 件衣服的子问题，总生产那时间也就减少为原来的一半。

生产衣服举例

所以原始问题是生产 1000 件衣服，子问题是两个生产 500 件衣服。子问题各自占用不同的流水线，所以他们互相是独立的，因此这是一个分治的思想。

分治算法的作用：

  • 简化思维逻辑：在很多情况下，原始问题是非常复杂的，例如排序问题。假设原始我们需要考虑对 1000 个数进行排序，那么利用分治思想我们可以分别对左右的 500 个数进行排序，然后考虑合并两个有序数组。当然，排序 500 个数看起来仍然不容易，但是我们可以继续分治下去，最终我们只需要考虑 1~2 个数的排序策略，这就是经典的归并排序的思想。

  • 分布式算法：虽然在算法学习的过程中少有接触多进程和分布式等思想。但是随着 CPU core 越来越多，能够被分治法拆解的问题显然更方便进行并行计算，从而节省总体时间。因此分治思想在工程实现上具有重要的意义。

小知识：在算法的学习过程中，经常有一种声音是质疑学习这些复杂的算法，实际上在工作中没什么作用。但是算法的学习本质上是一个积累和沉淀的过程，一方面我们可以锻炼出更高效和准确的思维和代码实现能力，另一方面在某些场景下也能尝试利用所学内容。比如我们可能会用分治 + 并行优化执行效率，也可能用分治 + 线段树优化查找效率。掌握好的算法思想，在某些工作场合能发挥出很大的作用。

  • 效率优化：虽然我们不常用并行解决算法问题，但是在某些情况下仍然能够帮助我们节省计算代价，代表就是快速幂算法。课程在这里不作展开，我们会在例题部分进一步详细讨论。

对于复杂的原问题：

  • 如果子问题最优则原问题最优，贪心算法。
  • 如果子问题需要全部求解才能求解原问题，子问题互相独立，分治算法。
  • 如果子问题最优不能保证原问题最优，但是子问题之间不会循环（所谓循环，是指从问题 A 拆解出子问题 B，然后子问题 B 又能拆解出子问题 A），考虑动态规划算法。
  • 更加复杂的情况，我们总是可以考虑暴力搜索解决。

动态规划

常用函数

C常用头文件

标准输入输出

1
2
3
#include < cstdio >
scanf()
printf()

标准库

1
2
#include < cstdlib >
qsort()

数学库

1
#include < cmath>

字符串库

1
2
#include < cstring >
memset(array_first_address, NUM, sizeof(array));

C++常用头文件

标准输入输出

1
2
3
4
#include < iostream >
using namespace std;
cin >>
cout <<

算法库

1
2
3
#include < algorithm >
next_permutation(array_first_address , array_first_address + length);
sort(array_first_address , array_first_address + length);

其他技巧 康托展开式公式: X=an*(n-1)!+an-1*(n-2)!+…+ai*(i-1)!+…+a2*1!+a1*0!

这个式子是由1到n这n个数组成的全排列，共n!个，按每个全排列组成的数从小到大进行排列，并对每个序列进行编号（从0开始）,并记为X。 比如说1到4组成的全排列中，长度为4，1234对应编号0，1243对应编号1 那a1,a2,a3,a4是什么意思呢？==>> 对1到4的全排列中，我们来考察3214，则 a4={3在集合(3,2,1,4)中是第几大的元素}=2 a3={2在集合(2,1,4)中是第几大的元素}=1 a2={1在集合(1,4)中是第几大的元素}=0 a1=0（最后只剩下一项） 则X=2×3!+1×2!+0×1!+0×0!=14，即3214对应的编号为14。 因此，此题用康托展开式就可以出来了，将abcd…写成1，2，3，4…就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
long long a[17];

long long fun(long long n) //求阶乘
{
    long long s = 1;
    for (int i = 1; i <= n; i++)
        s *= i;
    return s;
}

int main()
{
    long long t;
    int f[] = {2, 3, 11, 6, 17, 12, 1, 10, 8, 5, 13, 7, 9, 15, 4, 14, 16};
    long long sum = 0;

    a[0] = 1;
    for (int i = 1; i < 17; i++)
    {
        a[i] = a[i - 1] * i;
    }

    for (int i = 0; i < 16; i++)
    {
        t = 0;
        for (int j = i + 1; j < 17; j++)
        {
            if (f[j] < f[i])
            {
                t++;
            }
        }
        sum += (t)*a[17 - 1 - i]; //康托展开式公式
    }

    printf("%lld", sum);

    return 0;
}

sort()函数

sort函数用于C++中，对给定区间所有元素进行排序，默认为升序，也可进行降序排序。

一般是直接对数组进行排序，例如对数组a[10]排序，sort(a, a+10)。而sort函数的强大之处在可与cmp函数结合使用，即排序方法的选择。

为什么要用c++标准库里的排序函数？

sort()函数是c++一种排序方法之一，相较冒泡排序和选择排序所带来的执行效率不高的问题，sort()函数使用的排序方法是类似于快速排序的方法，时间复杂度为\(n×log_{2}(n)\)​，执行效率较高。

函数名 功能描述
sort 对给定区间所有元素进行排序
stable_sort 对给定区间所有元素进行稳定排序
partial_sort 对给定区间所有元素部分排序
partial_sort_copy 对给定区间复制并排序
nth_element 找出给定区间的某个位置对应的元素
is_sorted 判断一个区间是否已经排好序
partition 使得符合某个条件的元素放在前面
stable_partition 相对稳定的使得符合某个条件的元素放在前面

原帖地址：

蓝桥杯知识点汇总：基础知识和常用算法

参考文章：

LeetCode高频算法实战

#蓝桥杯
蓝桥杯C常用算法
https://excelius.xyz/蓝桥杯c常用算法/
作者
Ther
发布于
2021年3月20日
许可协议