PAT乙级备考

以下题目来源：https://pintia.cn/problem-sets/994805260223102976/problems/type/7

无特殊说明，题目来源不变。

PAT (Basic Level) Practice （中文）

1001 害死人不偿命的(3n+1)猜想 (15 分)

题目

卡拉兹(Callatz)猜想：

对任何一个正整数 n，如果它是偶数，那么把它砍掉一半；如果它是奇数，那么把 (3n+1) 砍掉一半。这样一直反复砍下去，最后一定在某一步得到 n=1。卡拉兹在 1950 年的世界数学家大会上公布了这个猜想，传说当时耶鲁大学师生齐动员，拼命想证明这个貌似很傻很天真的命题，结果闹得学生们无心学业，一心只证 (3n+1)，以至于有人说这是一个阴谋，卡拉兹是在蓄意延缓美国数学界教学与科研的进展……

我们今天的题目不是证明卡拉兹猜想，而是对给定的任一不超过 1000 的正整数 n，简单地数一下，需要多少步（砍几下）才能得到 n=1？

输入格式：

每个测试输入包含 1 个测试用例，即给出正整数 n 的值。

输出格式：

输出从 n 计算到 1 需要的步数。

输入样例：

输出样例：

题解

思路

根据题目直接写出判断代码即可，没有很难的地方......

代码

#include <iostream>

using namespace std;

// 3n+1 猜想
int main()
{
    int n;
    cin >> n;

    int num = 0;
    while (n > 1)
    {
        if (n % 2 == 0)
        {
            n = n / 2;
            num++;
        }
        else
        {
            n = (3 * n + 1) / 2;
            num++;
        }
    }
    cout << num << endl;

    return 0;
}

1002 写出这个数 (20 分)

题目

读入一个正整数 n，计算其各位数字之和，用汉语拼音写出和的每一位数字。

输入格式：

每个测试输入包含 1 个测试用例，即给出自然数 n 的值。这里保证 n 小于 10100。

输出格式：

在一行内输出 n 的各位数字之和的每一位，拼音数字间有 1 空格，但一行中最后一个拼音数字后没有空格。

输入样例：

1	`1234567890987654321123456789`

输出样例：

1	`yi san wu`

题解

思路

将输入的内容读取成字符串，然后每个位置转换成数字进行计算，再将数字结果转化为我们需要的结果即可。

代码

#include <iostream>
#include <algorithm>

using namespace std;

// 写出这个数
int main()
{
    string n;
    cin >> n;

    int len = n.length();
    int result = 0;

    for (int i = 0; i < len; i++)
    {
        result += n[i] - 48;
    }

    int res_n = 1;
    if (result >= 100)
    {
        res_n = 3;
    }
    else if (result >= 10)
    {
        res_n = 2;
    }

    while (res_n)
    {
        int t;
        switch (res_n)
        {
        case 3:
            t = result / 100;
            break;
        case 2:
            t = result / 10 % 10;
            break;
        case 1:
            t = result % 10;
            break;
        default:
            break;
        }
        res_n--;

        if (res_n >= 1)
        {
            switch (t)
            {
            case 0:
                cout << "ling ";
                break;
            case 1:
                cout << "yi ";
                break;
            case 2:
                cout << "er ";
                break;
            case 3:
                cout << "san ";
                break;
            case 4:
                cout << "si ";
                break;
            case 5:
                cout << "wu ";
                break;
            case 6:
                cout << "liu ";
                break;
            case 7:
                cout << "qi ";
                break;
            case 8:
                cout << "ba ";
                break;
            case 9:
                cout << "jiu ";
                break;
            default:
                break;
            }
        }
        else
        {
            switch (t)
            {
            case 0:
                cout << "ling";
                break;
            case 1:
                cout << "yi";
                break;
            case 2:
                cout << "er";
                break;
            case 3:
                cout << "san";
                break;
            case 4:
                cout << "si";
                break;
            case 5:
                cout << "wu";
                break;
            case 6:
                cout << "liu";
                break;
            case 7:
                cout << "qi";
                break;
            case 8:
                cout << "ba";
                break;
            case 9:
                cout << "jiu";
                break;
            default:
                break;
            }
        }
    }
    cout << endl;

    return 0;
}

代码优化小想法：感觉也可以用栈来解决存放问题，从左往右，先进先出。

1003

1004 成绩排名（20分）

题目

读入 n（>0）名学生的姓名、学号、成绩，分别输出成绩最高和成绩最低学生的姓名和学号。

输入格式：

每个测试输入包含 1 个测试用例，格式为

第 1 行：正整数 n
第 2 行：第 1 个学生的姓名 学号 成绩
第 3 行：第 2 个学生的姓名 学号 成绩
  ... ... ...
第 n+1 行：第 n 个学生的姓名 学号 成绩

其中姓名和学号均为不超过 10 个字符的字符串，成绩为 0 到 100 之间的一个整数，这里保证在一组测试用例中没有两个学生的成绩是相同的。

输出格式：

对每个测试用例输出 2 行，第 1 行是成绩最高学生的姓名和学号，第 2 行是成绩最低学生的姓名和学号，字符串间有 1 空格。

输入样例：

3
Joe Math990112 89
Mike CS991301 100
Mary EE990830 95

输出样例：

1 2	`Mike CS991301 Joe Math990112`

题解

思路

因为输入的特殊性，姓名、学号、成绩可以分开保存，这样只需要对成绩进行比较操作即可，记录我们要找的最大最小的下标，最后输出即可。

代码

#include <iostream>
#include <string>

using namespace std;

int main()
{
    // 输入
    int num;
    cin >> num;
    string input[3 * num];
    for (int i = 0; i < 3 * num; i++)
    {
        // 注意，这里输入的时候，会自动根据空格隔开，即第一行分为三个数组元素而不是一个
        // 因此上方数组元素的个数为3 * num
        cin >> input[i];
    }
    // 最大结果的成绩，下标
    int res_max_soc = 0;
    int res_max_index = 0;
    // 最小结果的成绩，下标
    int res_min_soc = 100;
    int res_min_index = 0;

    // 只需要比较成绩，故i从2开始，i每次增加三个值，然后比较，记录下标位置
    for (int i = 2; i < 3 * num; i = i + 3)
    {
        int temp = stoi(input[i]);
        if (temp >= res_max_soc)
        {
            res_max_soc = temp;
            res_max_index = i;
        }
        if (temp <= res_min_soc)
        {
            res_min_soc = temp;
            res_min_index = i;
        }
    }
    // 输出的结果只需要根据我们标记的下标值找到姓名学号即可
    cout << input[res_max_index - 2] << " " << input[res_max_index - 1] << endl;
    cout << input[res_min_index - 2] << " " << input[res_min_index - 1] << endl;

    return 0;
}

1005 继续(3n+1)猜想 (25 分)

题目

卡拉兹(Callatz)猜想已经在1001中给出了描述。在这个题目里，情况稍微有些复杂。

当我们验证卡拉兹猜想的时候，为了避免重复计算，可以记录下递推过程中遇到的每一个数。例如对 n=3 进行验证的时候，我们需要计算 3、5、8、4、2、1，则当我们对 n=5、8、4、2 进行验证的时候，就可以直接判定卡拉兹猜想的真伪，而不需要重复计算，因为这 4 个数已经在验证3的时候遇到过了，我们称 5、8、4、2 是被 3“覆盖”的数。我们称一个数列中的某个数 n 为“关键数”，如果 n 不能被数列中的其他数字所覆盖。

现在给定一系列待验证的数字，我们只需要验证其中的几个关键数，就可以不必再重复验证余下的数字。你的任务就是找出这些关键数字，并按从大到小的顺序输出它们。

输入格式：

每个测试输入包含 1 个测试用例，第 1 行给出一个正整数 K (<100)，第 2 行给出 K 个互不相同的待验证的正整数 n (1<n≤100)的值，数字间用空格隔开。

输出格式：

每个测试用例的输出占一行，按从大到小的顺序输出关键数字。数字间用 1 个空格隔开，但一行中最后一个数字后没有空格。

输入样例：

1 2	`6 3 5 6 7 8 11`

输出样例：

7 6

题解

思路

我的想法是，将每个数都做一遍3n+1猜想，然后重复出现的数，从容器中删除掉，最后排序输出即可，比较麻烦。网上有很多很聪明的代码，可以借鉴。

代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

// 查找函数
bool findNum(vector<int> input, int n, int &index)
{
    int len = input.size();
    for (int i = 0; i < len; i++)
    {
        if (input[i] == n)
        {
            index = i;
            return true;
        }
    }
    return false;
}

// 删除函数
void DeleteNum(vector<int> &input, int index)
{
    int len = input.size();
    for (int i = 0; i < len; i++)
    {
        if (i == index)
        {
            for (int j = i; j < len; j++)
            {
                input[j] = input[j + 1];
            }
            input.pop_back();
        }
    }
}

// 1005 继续(3n+1)猜想
int main()
{
    int count;
    cin >> count;
    vector<int> input(count);
    int t;
    for (int i = 0; i < count; i++)
    {
        cin >> input[i];
    }

    int i = 0;
    bool flag = false;
    while (i < count)
    {
        int n = input[i];
        while (n > 1)
        {
            if (n % 2 == 0)
            {
                n = n / 2;
                if (findNum(input, n, t))
                {
                    DeleteNum(input, t);
                    flag = true;
                    count--;
                }
            }
            else
            {
                n = (3 * n + 1) / 2;
                if (findNum(input, n, t))
                {
                    DeleteNum(input, t);
                    flag = true;
                    count--;
                }
            }
        }
        if (!flag)
            i++;
        flag = false;
    }

    // 输出
    sort(input.begin(), input.end());
    for (int i = count - 1; i >= 0; i--)
    {
        if (i != 0)
            cout << input[i] << " ";
        else
            cout << input[i];
    }

    return 0;
}

1006 换个格式输出整数 (15 分)

题目

让我们用字母 B 来表示“百”、字母 S 表示“十”，用 12...n 来表示不为零的个位数字 n（<10），换个格式来输出任一个不超过 3 位的正整数。例如 234 应该被输出为 BBSSS1234，因为它有 2 个“百”、3 个“十”、以及个位的 4。

输入格式：

每个测试输入包含 1 个测试用例，给出正整数 n（<1000）。

输出格式：

每个测试用例的输出占一行，用规定的格式输出 n。

输入样例 1：

输出样例 1：

1	`BBSSS1234`

输入样例 2：

输出样例 2：

SS123

题解

思路

一开始以为输出的结果为：

百位数字个的B + 十位数字个的S + 1 + 输入的内容

但后来研究了一下，才发现正确的是这样的：

百位数字个的B + 十位数字个的S + 从1输出到个位数字

那么代码就很明确了：

代码

#include <iostream>

using namespace std;

int main()
{
    int input;
    cin >> input;

    int bai = input / 100;
    int shi = input / 10 % 10;
    int ge = input % 10;

    for (int i = 0; i < bai; i++)
    {
        cout << "B";
    }
    for (int i = 0; i < shi; i++)
    {
        cout << "S";
    }
    for (int i = 1; i <= ge; i++)
    {
        cout << i;
    }

    return 0;
}

1007 素数对猜想 (20 分)

题目

让我们定义dn为：dn=pn+1−pn，其中pi是第i个素数。显然有d1=1，且对于n>1有dn是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。

现给定任意正整数N(<10^5)，请计算不超过N的满足猜想的素数对的个数。

输入格式:

输入在一行给出正整数N。

输出格式:

在一行中输出不超过N的满足猜想的素数对的个数。

输入样例:

输出样例:

题解

思路

根据题目的要求，借助输入的N找到所有小于等于N的素数prime[]，然后再判断prime[i+1]-prime[i]的值即可。

思路二：

从0到N遍历一下，然后用个数组标记是否是素数，是为1，不是为0。再判断x[i+1]-x[i]即可。

代码

#include <iostream>
#include <vector>
#include <math.h>

using namespace std;

void GetPrime(long &num, long n, long prime[100000])
{
    for (long i = 0; i <= n; i++)
    {
        long j = 2, sqrti = sqrt(i);
        for (; j <= sqrti; j++)
        {
            if (i % j == 0)
            {
                break;
            }
        }
        if (j > sqrti)
        {
            prime[num++] = i;
        }
    }
}

void GetRes(long num, long prime[])
{
    long res = 0;
    for (long i = 0; i < num - 1; i++)
    {
        if (prime[i + 1] - prime[i] == 2)
        {
            res++;
        }
    }
    cout << res;
}

int main()
{
    long n, num = 0;
    cin >> n;
    long prime[100000];

    if (n == 1 || n == 2 || n == 3 || n == 4)
    {
        cout << "0";
    }
    else
    {
        GetPrime(num, n, prime);
        GetRes(num, prime);
    }

    system("pause");
    return 0;
}

1008 数组元素循环右移问题 (20 分)

题目

一个数组A中存有N（>0）个整数，在不允许使用另外数组的前提下，将每个整数循环向右移M（≥0）个位置，即将A中的数据由（A0A1⋯AN−1）变换为（AN−M⋯AN−1A0A1⋯AN−M−1）（最后M个数循环移至最前面的M个位置）。如果需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

输入格式:

每个输入包含一个测试用例，第1行输入N（1≤N≤100）和M（≥0）；第2行输入N个整数，之间用空格分隔。

输出格式:

在一行中输出循环右移M位以后的整数序列，之间用空格分隔，序列结尾不能有多余空格。

输入样例:

1 2	`6 2 1 2 3 4 5 6`

输出样例:

1	`5 6 1 2 3 4`

题解

思路

本来想着根据题目交换数据来着，后来第一次AC没通过之后发现，为什么要交换呢？输出的结果不一定必须体现出交换的这个步骤，只要方法得当，只把结果输出也是可以的。而且这个规律很好找。有个需要注意的点就是，m如果比n大的话，需要m对n求余，因为m等于n的时候，移动后跟原本一模一样。下面的代码如果不求余会出现错误（数组越界输出）。

代码

#include <iostream>

using namespace std;

int main()
{
    int num, index;
    cin >> num >> index;

    int *input = new int[num];
    for (int i = 0; i < num; i++)
    {
        cin >> input[i];
    }

    index = index % num;

    int count = 0;
    for (int i = num - index; i < num; i++)
    {
        if (count != num - 1)
        {
            cout << input[i] << " ";
            count++;
        }
        else
        {
            cout << input[i];
            count++;
        }
    }
    for (int i = 0; i < num - index; i++)
    {
        if (count != num - 1)
        {
            cout << input[i] << " ";
            count++;
        }
        else
        {
            cout << input[i];
            count++;
        }
    }

    system("pause");
    return 0;
}

1009 说反话 (20 分)

题目

给定一句英语，要求你编写程序，将句中所有单词的顺序颠倒输出。

输入格式：

测试输入包含一个测试用例，在一行内给出总长度不超过 80 的字符串。字符串由若干单词和若干空格组成，其中单词是由英文字母（大小写有区分）组成的字符串，单词之间用 1 个空格分开，输入保证句子末尾没有多余的空格。

输出格式：

每个测试用例的输出占一行，输出倒序后的句子。

输入样例：

1	`Hello World Here I Come`

输出样例：

1	`Come I Here World Hello`

题解

本来想着将字符串分割的，后来在网上看到一个十分巧妙的做法，自愧不如，放上看到的代码。

巧妙的地方在于，没有将字符串进行分割，而是借助cin将空格作为分隔符，直接将输入的单词进行拼接输出。orz。

//利用string对输入单词进行拼接
#include <iostream>
#include <string>
using namespace std;

int main()
{
    string in, out;
    cin >> out;
    while (cin >> in)
    {
        out = in + " " + out;
    }
    cout << out << endl;

    system("pause");
    return 0;
}

1010 一元多项式求导（25分）

题目

设计函数求一元多项式的导数。（注：x^n（n为整数）的一阶导数为nx^n−1。）

输入格式:

以指数递降方式输入多项式非零项系数和指数（绝对值均为不超过 1000 的整数）。数字间以空格分隔。

输出格式:

以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔，但结尾不能有多余空格。注意“零多项式”的指数和系数都是 0，但是表示为 0 0。

输入样例:

1	`3 4 -5 2 6 1 -2 0`

输出样例:

1	`12 3 -10 1 6 0`

题解

有坑的地方是：当输入空串时，要输出0 0。系数非0，指数为0为空串。

代码

#include <iostream>
int main()
{
    int a, b;
    int count = 0;
    while (scanf("%d %d", &a, &b) != EOF)
    {
        if (b != 0)
            count++;
        // 输入空串，输出0 0
        if (count == 0)
        {
            printf("0 0");
            return 0;
        }
        if (b != 0)
        {
            if (count != 1)
                printf(" ");
            printf("%d %d", a * b, b - 1);
        }
    }

    system("pause");
    return 0;
}

1011 A+B 和 C (15 分)

题目

给定区间 [−2^31,231] 内的 3 个整数 A、B 和 C，请判断 A+B 是否大于 C。

输入格式：

输入第 1 行给出正整数 T (≤10)，是测试用例的个数。随后给出 T 组测试用例，每组占一行，顺序给出 A、B 和 C。整数间以空格分隔。

输出格式：

对每组测试用例，在一行中输出 Case #X: true 如果 A+B>C，否则输出 Case #X: false，其中 X 是测试用例的编号（从 1 开始）。

输入样例：

4
1 2 3
2 3 4
2147483647 0 2147483646
0 -2147483648 -2147483647

输出样例：

Case #1: false
Case #2: true
Case #3: true
Case #4: false

题解

本题很简单，本来以为只有输入完后才可以输出，后来测试到不输入完也可以输出，那就很nice了，一个循环解决，double够用，注意英文:后面有个空格。

代码

#include <iostream>

using namespace std;

int main()
{
    int num = 0;
    cin >> num;
    double inputA[10] = {0};
    double inputB[10] = {0};
    double inputC[10] = {0};
    for (int i = 0; i < num; i++)
    {
        cin >> inputA[i] >> inputB[i] >> inputC[i];
        if (inputA[i] + inputB[i] > inputC[i])
        {
            cout << "Case #" << i + 1 << ": true" << endl;
        }
        else
        {
            cout << "Case #" << i + 1 << ": false" << endl;
        }
    }

    return 0;
}

1012 数字分类 (20 分)

题目

给定一系列正整数，请按要求对数字进行分类，并输出以下 5 个数字：

A1 = 能被 5 整除的数字中所有偶数的和；
A2 = 将被 5 除后余 1 的数字按给出顺序进行交错求和，即计算 n1−n2+n3−n4⋯；
A3 = 被 5 除后余 2 的数字的个数；
A4 = 被 5 除后余 3 的数字的平均数，精确到小数点后 1 位；
A5 = 被 5 除后余 4 的数字中最大数字。

输入格式：

每个输入包含 1 个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N，随后给出 N 个不超过 1000 的待分类的正整数。数字间以空格分隔。

输出格式：

对给定的 N 个正整数，按题目要求计算 A1~A5 并在一行中顺序输出。数字间以空格分隔，但行末不得有多余空格。

若其中某一类数字不存在，则在相应位置输出 N。

输入样例 1：

1	`13 1 2 3 4 5 6 7 8 9 10 20 16 18`

输出样例 1：

1	`30 11 2 9.7 9`

输入样例 2：

1	`8 1 2 4 5 6 7 9 16`

输出样例 2：

1	`N 11 2 N 9`

题解

该题根据题目的要求，使用判断条件即可，需要注意的是，最后一个测试点，不能单纯使用num1 == 0来判断，因为可能会出现和值为0的情况，需要另外的标记变量，标记一下该类变量的出现次数。

代码

#include <iostream>
#include <vector>
#include <iomanip>

using namespace std;

int main()
{
    long temp = 0;
    vector<long> input;
    int flag[5] = {0};

    while (cin >> temp)
    {
        input.push_back(temp);
    }

    int index = 1;
    double sum0 = 0, sum1 = 0, num2 = 0, sum3 = 0, num3 = 0, num4 = 0;
    for (int i = 1; i < input.size(); i++)
    {
        if (input[i] % 5 == 0)
        {
            if (input[i] % 2 == 0)
            {
                sum0 += input[i];
                flag[0] = 1;
            }
        }
        else if (input[i] % 5 == 1)
        {
            if (index % 2 == 0)
            {
                sum1 -= input[i];
                index++;
                flag[1] = 1;
            }
            else
            {
                sum1 += input[i];
                index++;
                flag[1] = 1;
            }
        }
        // 被 5 除后余 2 的数字的个数
        else if (input[i] % 5 == 2)
        {
            num2++;
            flag[2] = 1;
        }
        // 被 5 除后余 3 的数字的平均数，精确到小数点后 1 位
        else if (input[i] % 5 == 3)
        {
            sum3 += input[i];
            num3++;
            flag[3] = 1;
        }
        // 被 5 除后余 4 的数字中最大数字
        else
        {
            if (input[i] >= num4)
            {
                num4 = input[i];
                flag[4] = 1;
            }
        }
    }

    if (flag[0] != 0)
    {
        cout << sum0 << " ";
    }
    else
    {
        cout << "N ";
    }

    if (flag[1] != 0)
    {
        cout << sum1 << " ";
    }
    else
    {
        cout << "N ";
    }

    if (flag[2] != 0)
    {
        cout << num2 << " ";
    }
    else
    {
        cout << "N ";
    }

    if (flag[3] != 0)
    {
        cout << fixed << setprecision(1) << sum3 / num3 << " ";
    }
    else
    {
        cout << "N ";
    }

    if (flag[4] != 0)
    {
        cout << (int)num4;
    }
    else
    {
        cout << "N";
    }

    system("pause");
    return 0;
}

1013 数素数 (20 分)

题目

令 Pi 表示第 i 个素数。现任给两个正整数 M≤N≤10^4，请输出 PM 到 PN 的所有素数。

输入格式：

输入在一行中给出 M 和 N，其间以空格分隔。

输出格式：

输出从 PM 到 PN 的所有素数，每 10 个数字占 1 行，其间以空格分隔，但行末不得有多余空格。

输入样例：

5 27

输出样例：

1
2
3

11 13 17 19 23 29 31 37 41 43
47 53 59 61 67 71 73 79 83 89
97 101 103

题解

题目很简单，但是因为数据比较大，所以数组要开大点，而且测试用例四的数据至少要在105000以上。

代码

#include <iostream>
#include <math.h>

using namespace std;

int main()
{
    long pri[107000] = {0};
    bool isPri[107000] = {false};
    int m = 0, n = 0;

    cin >> m >> n;

    for (long i = 2; i < 107000; i++)
    {
        pri[i] = i;
        int j = 2;
        for (; j <= sqrt(i); j++)
        {
            if (i % j == 0)
            {
                break;
            }
        }

        // 是素数
        if (j > sqrt(i))
        {
            isPri[i] = true;
        }
    }

    int index = 0, num = 0;
    for (long i = 0; i < 107000; i++)
    {
        if (isPri[i])
        {
            index++;

            if (m <= index && index <= n)
            {
                if (num == 0)
                {
                    cout << pri[i];
                    num++;
                }
                else
                {
                    cout << " " << pri[i];
                    num++;
                    if (num == 10 && index != n)
                    {
                        cout << endl;
                        num = 0;
                    }
                }
            }
        }
    }

    system("pause");
    return 0;
}

1014 福尔摩斯的约会 (20 分)

题目

大侦探福尔摩斯接到一张奇怪的字条：我们约会吧！ 3485djDkxh4hhGE 2984akDfkkkkggEdsb s&hgsfdk d&Hyscvnm。大侦探很快就明白了，字条上奇怪的乱码实际上就是约会的时间星期四 14:04，因为前面两字符串中第 1 对相同的大写英文字母（大小写有区分）是第 4 个字母 D，代表星期四；第 2 对相同的字符是 E ，那是第 5 个英文字母，代表一天里的第 14 个钟头（于是一天的 0 点到 23 点由数字 0 到 9、以及大写字母 A 到 N 表示）；后面两字符串第 1 对相同的英文字母 s 出现在第 4 个位置（从 0 开始计数）上，代表第 4 分钟。现给定两对字符串，请帮助福尔摩斯解码得到约会的时间。

输入格式：

输入在 4 行中分别给出 4 个非空、不包含空格、且长度不超过 60 的字符串。

输出格式：

在一行中输出约会的时间，格式为 DAY HH:MM，其中 DAY 是某星期的 3 字符缩写，即 MON 表示星期一，TUE 表示星期二，WED 表示星期三，THU 表示星期四，FRI 表示星期五，SAT 表示星期六，SUN 表示星期日。题目输入保证每个测试存在唯一解。

输入样例：

3485djDkxh4hhGE 
2984akDfkkkkggEdsb 
s&hgsfdk 
d&Hyscvnm

输出样例：

1	`THU 14:04`

题解

该题的思路还是挺清晰的，首先按照步骤走：

根据前两个字符串相等的大写字母的位置确定周几
在第一步的基础上再往后走，判断小时
最后根据最后两个字符串确定分钟

这里需要注意的边界值或者条件有：

小时找到之后便不需要再遍历，直接跳出
分钟找到之后也需要跳出，无需再遍历
60分钟要变成0且小时加一
没有24H，24要改为0H

代码

#include <iostream>
#include <iomanip>

using namespace std;

int main()
{
    string s1 = "";
    string s2 = "";
    string s3 = "";
    string s4 = "";
    string week[] = {"MON", "TUE", "WED", "THU", "FRI", "SAT", "SUN"};
    int hour = 0, minute = 0;

    cin >> s1 >> s2 >> s3 >> s4;

    int len1 = s1.length() > s2.length() ? s2.length() : s1.length();
    int flag = 0;
    for (int i = 0; i < len1; i++)
    {
        // flag为 0 要输出周几
        if (!flag)
        {
            if (s1[i] == s2[i] && (s1[i] >= 'A' && s1[i] <= 'G'))
            {
                cout << week[s1[i] - 'A'] << " ";
                flag = 1;
            }
        }
        // 可以输出小时了
        else if (flag == 1)
        {
            // 0-9要输出0x的格式
            if (s1[i] == s2[i] && ('0' <= s1[i] && s1[i] <= '9'))
            {
                hour = s1[i] - '0';
                // 要跳出循环
                break;
            }
            else if (s1[i] == s2[i] && ('A' <= s1[i] && s1[i] <= 'N'))
            {
                hour = s1[i] - 'A' + 10;
                // 要跳出循环
                break;
            }
        }
    }

    int len2 = s3.length() > s4.length() ? s4.length() : s3.length();
    for (int i = 0; i < len2; i++)
    {
        if (s3[i] == s4[i] && ((s3[i] >= 'A' && s3[i] <= 'Z') || (s3[i] >= 'a' && s3[i] <= 'z')))
        {
            minute = i;
            break;
        }
    }

    if (minute == 60)
    {
        minute = 0;
        hour++;
    }

    if (hour == 24)
    {
        hour = 0;
    }

    if (hour < 10)
    {
        cout << "0" << hour << ":";
    }
    else
    {
        cout << hour << ":";
    }

    if (minute < 10)
    {
        cout << "0" << minute;
    }
    else
    {
        cout << minute;
    }

    system("pause");
    return 0;
}

1015

1016 部分A+B (15 分)

题目

正整数 A 的Da（为 1 位整数）部分定义为由 A 中所有 Da 组成的新整数 Pa。例如：给定 A=3862767，Da=6，则 A 的6 部分Pa 是 66，因为 A 中有 2 个 6。

现给定 A、Da、B、Db，请编写程序计算 Pa+Pb。

输入格式：

输入在一行中依次给出 A、Da、B、Db，中间以空格分隔，其中 0<A,B<109。

输出格式：

在一行中输出 Pa+Pb 的值。

输入样例 1：

1	`3862767 6 13530293 3`

输出样例 1：

输入样例 2：

1	`3862767 1 13530293 8`

输出样例 2：

题解

这道题目比较中规中矩，按照题目说得来就行。输入的a，b用string类型处理比较方便，因为需要获取每位上的值嘛，字符跟数字的比较要先处理一下s[i]-48。

代码

#include <iostream>

using namespace std;

long GetP(string s, long d)
{
    long p = 0;
    int len = s.length();
    int temp = 1;
    for (int i = 0; i < len; i++)
    {
        if (s[i] - 48 == d)
        {
            p += d * temp;
            temp *= 10;
        }
    }
    return p;
}

int main()
{
    string a = "", b = "";
    long da = 0, db = 0;

    cin >> a >> da >> b >> db;

    cout << GetP(a, da) + GetP(b, db) << endl;

    system("pause");
    return 0;
}

1017

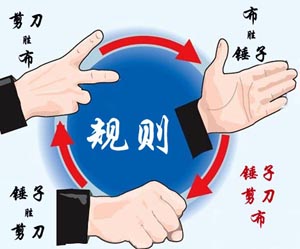
1018 锤子剪刀布 (20 分)

题目

大家应该都会玩“锤子剪刀布”的游戏：两人同时给出手势，胜负规则如图所示：

现给出两人的交锋记录，请统计双方的胜、平、负次数，并且给出双方分别出什么手势的胜算最大。

输入格式：

输入第 1 行给出正整数 N（≤105），即双方交锋的次数。随后 N 行，每行给出一次交锋的信息，即甲、乙双方同时给出的的手势。C 代表“锤子”、J 代表“剪刀”、B 代表“布”，第 1 个字母代表甲方，第 2 个代表乙方，中间有 1 个空格。

输出格式：

输出第 1、2 行分别给出甲、乙的胜、平、负次数，数字间以 1 个空格分隔。第 3 行给出两个字母，分别代表甲、乙获胜次数最多的手势，中间有 1 个空格。如果解不唯一，则输出按字母序最小的解。

输入样例：

10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J

输出样例：

1
2
3

5 3 2
2 3 5
B B

题解

思路

题目理解起来并不复杂，首先弄好输入，一个num变量，一个jia数组，一个yi数组，然后就是判断胜负次数，我是根据每次jia-yi来计算的。最后是输出胜最多的字符，因为事先规定了hand数组的位置hand[0]：J，hand[1]：C，hand[2]：B，所以只需要hand[i] >= max，记录此时的i值，就可以顺便记录到多次解取字母最小的解。

代码

#include <iostream>

using namespace std;

// 返回值：0-甲胜，1-乙胜，2-平局
int isWin(char jia, char yi, int jiaWinHand[3], int yiWinHand[3])
{
    int res = -1;
    // 因为jia-yi的值全不一样（除了平局），因此可以借助差值判断胜负
    switch (jia - yi)
    {
    // 平局
    case 0:
        return 2;
        break;
    // 甲胜（乙输）
    case -7:
        // 锤胜
        jiaWinHand[1]++;
        res = 0;
        break;
    case 8:
        // 剪刀胜
        jiaWinHand[0]++;
        res = 0;
        break;
    case -1:
        // 布胜
        jiaWinHand[2]++;
        res = 0;
        break;
    // 甲输（乙胜）
    case 1:
        // 布胜
        yiWinHand[2]++;
        res = 1;
        break;
    case 7:
        // 锤胜
        yiWinHand[1]++;
        res = 1;
        break;
    case -8:
        // 剪刀胜
        yiWinHand[0]++;
        res = 1;
        break;
    default:
        break;
    }
    return res;
}

char GetWinHand(int hand[3])
{
    char res;

    int max = INT16_MIN, index = -1;
    for (int i = 0; i < 3; i++)
    {
        if (hand[i] >= max)
        {
            max = hand[i];
            index = i;
        }
    }

    switch (index)
    {
    case 0:
        res = 'J';
        break;
    case 1:
        res = 'C';
        break;
    case 2:
        res = 'B';
        break;
    default:
        break;
    }

    return res;
}

int main()
{
    long count;
    cin >> count;
    char *jia = new char[count];
    char *yi = new char[count];

    for (int i = 0; i < count; i++)
    {
        cin >> jia[i] >> yi[i];
    }

    int jiaWin = 0;
    // x[0]：剪刀，x[1]：石头，x[2]：布
    int jiaWinHead[] = {0, 0, 0};
    int yiWinHead[] = {0, 0, 0};
    int yiWin = 0;
    int winWin = 0;
    for (int i = 0; i < count; i++)
    {
        // cout << jia[i] << " " << yi[i] << " " << isWin(jia[i], yi[i]) << endl;
        switch (isWin(jia[i], yi[i], jiaWinHead, yiWinHead))
        {
        case 0:
            jiaWin++;
            break;
        case 1:
            yiWin++;
            break;
        case 2:
            winWin++;
            break;
        default:
            break;
        }
    }

    cout << jiaWin << " " << winWin << " " << count - jiaWin - winWin << endl;
    cout << yiWin << " " << winWin << " " << count - yiWin - winWin << endl;

    cout << GetWinHand(jiaWinHead) << " " << GetWinHand(yiWinHead);

    system("pause");
    return 0;
}

《蛤蟆先生去看心理医生》书还挺不错的，心理学的书可以多看看，也是认识自己的一种方式。

1019 数字黑洞 (20 分)

题目

给定任一个各位数字不完全相同的 4 位正整数，如果我们先把 4 个数字按非递增排序，再按非递减排序，然后用第 1 个数字减第 2 个数字，将得到一个新的数字。一直重复这样做，我们很快会停在有“数字黑洞”之称的 6174，这个神奇的数字也叫 Kaprekar 常数。

例如，我们从6767开始，将得到

7766 - 6677 = 1089
9810 - 0189 = 9621
9621 - 1269 = 8352
8532 - 2358 = 6174
7641 - 1467 = 6174
... ...

现给定任意 4 位正整数，请编写程序演示到达黑洞的过程。

输入格式：

输入给出一个 (0,104) 区间内的正整数 N。

输出格式：

如果 N 的 4 位数字全相等，则在一行内输出 N - N = 0000；否则将计算的每一步在一行内输出，直到 6174 作为差出现，输出格式见样例。注意每个数字按 4 位数格式输出。

输入样例 1：

1 2	`6767 结尾无空行`

输出样例 1：

7766 - 6677 = 1089
9810 - 0189 = 9621
9621 - 1269 = 8352
8532 - 2358 = 6174
结尾无空行

输入样例 2：

1 2	`2222 结尾无空行`

输出样例 2：

1 2	`2222 - 2222 = 0000 结尾无空行`

题解

思路

这道题目根据题目意思写出代码，一般6767是可以跑出来的。需要注意的是：

如果输入的不足四位，要补足四位；
如果过程中出现不足四位，也要补足；
控制格式化输出，字符串转整型运算，整型转字符串。

代码

#include <iostream>
#include <algorithm>
#include <iomanip>

using namespace std;

bool cmp(char a, char b)
{
    return a > b;
}

// 数字黑洞
int main()
{
    string input;
    cin >> input;

    int big = 0, small = 0, res = -1;

    do
    {
        // 不足四位补足
        int len = input.length();
        input.append(4 - len, '0');
        
        sort(input.begin(), input.end());
        string rev = input;
        reverse(rev.begin(), rev.end());
        big = stoi(rev);
        small = stoi(input);
        res = big - small;
        cout << setw(4) << setfill('0') << big << " - " << setw(4) << setfill('0') << small
             << " = " << setw(4) << setfill('0') << res << endl;
        input = to_string(res);
    } while (res != 6174 && res != 0);

    system("pause");
    return 0;
}

1020 月饼 (25 分)

题目

月饼是中国人在中秋佳节时吃的一种传统食品，不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量，请你计算可以获得的最大收益是多少。

注意：销售时允许取出一部分库存。样例给出的情形是这样的：假如我们有 3 种月饼，其库存量分别为 18、15、10 万吨，总售价分别为 75、72、45 亿元。如果市场的最大需求量只有 20 万吨，那么我们最大收益策略应该是卖出全部 15 万吨第 2 种月饼、以及 5 万吨第 3 种月饼，获得 72 + 45/2 = 94.5（亿元）。

输入格式：

每个输入包含一个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N 表示月饼的种类数、以及不超过 500（以万吨为单位）的正整数 D 表示市场最大需求量。随后一行给出 N 个正数表示每种月饼的库存量（以万吨为单位）；最后一行给出 N 个正数表示每种月饼的总售价（以亿元为单位）。数字间以空格分隔。

输出格式：

对每组测试用例，在一行中输出最大收益，以亿元为单位并精确到小数点后 2 位。

输入样例：

输出样例：

1 2	`94.50 结尾无空行`

题解

思路

考虑到本题有排序的性质，弄一个结构体会比较方便。

设置的结构体为：

struct Cake
{
    double rep;			// 库存
    double val;			// 总价
    double eachVal;		// 单价
};

输入完成后就可以排序了，使用的是algorithm.h里的sort()函数。

排序完成后，累加rep与maxNeed比较，找到末尾的值，最后控制格式输出即可。需要注意的是数组不要越界。

代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <iomanip>

using namespace std;

struct Cake
{
    double rep;
    double val;
    double eachVal;
};

// a的单位价值大于b的单位价值，返回真
bool cmp(Cake a, Cake b)
{
    return a.eachVal > b.eachVal;
}

int main()
{
    int count = 0, maxNeed = 0;

    cin >> count >> maxNeed;

    vector<Cake> cake(count);

    for (int i = 0; i < count; i++)
    {
        cin >> cake[i].rep;
    }

    for (int i = 0; i < count; i++)
    {
        cin >> cake[i].val;
        cake[i].eachVal = cake[i].val / cake[i].rep;
    }

    sort(cake.begin(), cake.end(), cmp);

    double used = 0, res = 0;
    int index = 0;
    while (used <= maxNeed && index < count)
    {
        if (used + cake[index].rep < maxNeed)
        {
            used += cake[index].rep;
            res += cake[index].val;
            index++;
        }
        else
        {
            break;
        }
    }
    cout << fixed << setprecision(2) << res + ( maxNeed - used ) * cake[index].eachVal << endl;

    system("pause");
    return 0;
}

1021 个位数统计 (15 分)

题目

给定一个 k 位整数 \[ N=d_{k−1}10^{k−1}+⋯+d_{1}10^{1}+d_0 \quad (0≤d_i≤9, i=0,⋯,k−1, d_{k−1}>0) \] 请编写程序统计每种不同的个位数字出现的次数。例如：给定 N=100311，则有 2 个 0，3 个 1，和 1 个 3。

输入格式：

每个输入包含 1 个测试用例，即一个不超过 1000 位的正整数 N。

输出格式：

对 N 中每一种不同的个位数字，以 D:M 的格式在一行中输出该位数字 D 及其在 N 中出现的次数 M。要求按 D 的升序输出。

输入样例：

输出样例：

1
2
3

0:2
1:3
3:1

题解

思路

这道题目因为输入不超过一千位的数，所以常见的数值类型都不可以，用string即可。然后使用sort()方法对s排序，这里是自定义了一个cmp规则，根据该规则，小数字在前面，然后便可以进行统计个数了，自定义一个结构体变量Count保存统计的信息，代码看起来还是很清晰的。

代码

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

bool cmp(char a, char b)
{
    return a < b;
}

struct Count
{
    int num;
    int amount;
};

int main()
{
    string s;

    cin >> s;

    int count = s.length();

    sort(s.begin(), s.end(), cmp);

    vector<Count> vec;
    int index = 0;
    for (int i = 0; i < count; i++)
    {
        int len = vec.size();
        if (len == 0)
        {
            Count temp;
            temp.num = s[i] - 48;
            temp.amount = 1;
            vec.push_back(temp);
        }
        else
        {
            if (vec[index].num == s[i] - 48)
            {
                vec[index].amount++;
            }
            else
            {
                Count temp;
                temp.num = s[i] - 48;
                temp.amount = 1;
                vec.push_back(temp);
                index++;
            }
        }
    }

    for (int i = 0; i < vec.size(); i++)
    {
        cout << vec[i].num << ":" << vec[i].amount << endl;
    }

    system("pause");
    return 0;
}

1022 D进制的A+B (20 分)

题目

输入两个非负 10 进制整数 A 和 B (≤ $2^{30}−1$)，输出 A+B 的 D (1<D≤10)进制数。

MarkDown输入行内公式：行内输入$+esc

输入格式：

输入在一行中依次给出 3 个整数 A、B 和 D。

输出格式：

输出 A+B 的 D 进制数。

输入样例：

1	`123 456 8`

输出样例：

题解

思路

按部就班做就好，这题不难。首先输入的A，B是十进制数，A+B的结果假设为C也是十进制数，十进制转八进制循环相除取余即可，但要记住类似栈，先进后出，所以使用STL中的stack解决该问题。

代码

#include <iostream>
#include <stack>

using namespace std;

int main()
{
    long long a = 0, b = 0, c = 0;
    int d = 0;

    cin >> a >> b >> d;

    c = a + b;
    stack<long long> s;
    while (c / d)
    {
        s.push(c % d);
        c = c / d;
    }
    s.push(c % d);

    int len = s.size();
    for (int i = 0; i < len; i++)
    {
        cout << s.top();
        s.pop();
    }

    system("pause");
    return 0;
}

1023 组个最小数 (20 分)

题目

给定数字 0-9 各若干个。你可以以任意顺序排列这些数字，但必须全部使用。目标是使得最后得到的数尽可能小（注意 0 不能做首位）。例如：给定两个 0，两个 1，三个 5，一个 8，我们得到的最小的数就是 10015558。

现给定数字，请编写程序输出能够组成的最小的数。

输入格式：

输入在一行中给出 10 个非负整数，顺序表示我们拥有数字 0、数字 1、……数字 9 的个数。整数间用一个空格分隔。10 个数字的总个数不超过 50，且至少拥有 1 个非 0 的数字。

输出格式：

在一行中输出能够组成的最小的数。

输入样例：

1	`2 2 0 0 0 3 0 0 1 0`

输出样例：

1	`10015558`

题解

思路

代码

#include <iostream>
#include <algorithm>

using namespace std;

int main()
{
    int num[10] = {0};
    string s;
    // C++输入一行
    for (int i = 0; i < 10; i++)
    {
        cin >> num[i];
    }

    string res = "";
    bool flag = true;
    int index = -1, len = 0;
    for (int i = 0; i < 10; i++)
    {
        if (num[i] != 0)
        {
            for (int j = 0; j < num[i]; j++)
            {
                res += to_string(i);
                len++;
                if (flag && i != 0)
                {
                    index = len - 1;
                    flag = false;
                }
            }
        }
    }
    swap(res[0], res[index]);

    res == "" || index == -1 ? cout << 0 : cout << res;

    system("pause");
    return 0;
}

1024 科学计数法 (20 分)

题目

科学计数法是科学家用来表示很大或很小的数字的一种方便的方法，其满足正则表达式[+-][1-9].[0-9]+E[+-][0-9]+，即数字的整数部分只有 1 位，小数部分至少有 1 位，该数字及其指数部分的正负号即使对正数也必定明确给出。

现以科学计数法的格式给出实数 A，请编写程序按普通数字表示法输出 A，并保证所有有效位都被保留。

输入格式：

每个输入包含 1 个测试用例，即一个以科学计数法表示的实数 A。该数字的存储长度不超过 9999 字节，且其指数的绝对值不超过 9999。

输出格式：

对每个测试用例，在一行中按普通数字表示法输出 A，并保证所有有效位都被保留，包括末尾的 0。

输入样例 1：

1	`+1.23400E-03`

输出样例 1：

1	`0.00123400`

输入样例 2：

1	`-1.2E+10`

输出样例 2：

1	`-12000000000`

题解

思路

指数为正为负分开讨论（临界值：小数长度与指数长度相等时）

指数为0

代码

#include <iostream>
#include <algorithm>

using namespace std;

int main()
{
    string s;
    cin >> s;

    int len = s.size();
    // E 所在位置的下标
    int eIndex = 0;
    // 整数的符号
    char symInt = s[0];
    // 因为整数不为0，所以整数可以直接提取
    string integer = s.substr(1, 1);
    // 小数部分
    string dec = "";
    // 指数部分字符串形式
    string sIndex = "";
    // 指数符号
    char symInd;
    // 因为指数的绝对值不超过9999，所以从后往前找 E 的位置，然后切割字符串
    for (int i = s.size() - 1; i > 0; i--)
    {
        // 找到了给一系列变量赋值
        if (s[i] == 'E')
        {
            eIndex = i;
            sIndex = s.substr(i + 2);
            symInd = s[i + 1];
            dec = s.substr(3, i - 3);
            break;
        }
    }
	// 指数转换成整数型，以便0的添加与删除
    int nIndex = stoi(sIndex);
	// 输出符号
    if (symInt == '-')
    {
        cout << '-';
    }

    int lenDec = dec.size();
    // 指数为0的情况单独考虑
    if (nIndex == 0)
    {
        cout << 1;
        // 因为小数部分至少有一位，那么存在-1.0E+1类似的情况
        for (int i = 0; i < lenDec + 1; i++)
        {
            if (i == 0)
            {
                cout << '.';
            }
            else
            {
                cout << 0;
            }
        }

        system("pause");
        return 0;
    }
	
    // 指数为正
    if (symInd == '+')
    {
        cout << integer;
        if (lenDec > nIndex)
        {
            for (int i = 0; i < nIndex; i++)
            {
                cout << dec[i];
            }
            cout << '.';
            cout << dec.substr(nIndex);
        }
        else
        {
            cout << dec;
            for (int i = 0; i < nIndex - lenDec; i++)
            {
                cout << '0';
            }
        }
    }
    else
    {
        for (int i = 0; i < nIndex + 1; i++)
        {
            if (i == 1)
            {
                cout << '.';
            }
            else
            {
                cout << '0';
            }
        }
        cout << integer << dec;
    }

    system("pause");
    return 0;
}

1025 反转链表 (25 分)

题目

给定一个常数 K 以及一个单链表 L，请编写程序将 L 中每 K 个结点反转。例如：给定 L 为 1→2→3→4→5→6，K 为 3，则输出应该为 3→2→1→6→5→4；如果 K 为 4，则输出应该为 4→3→2→1→5→6，即最后不到 K 个元素不反转。

输入格式：

每个输入包含 1 个测试用例。每个测试用例第 1 行给出第 1 个结点的地址、结点总个数正整数 N (≤105)、以及正整数 K (≤N)，即要求反转的子链结点的个数。结点的地址是 5 位非负整数，NULL 地址用 −1 表示。

接下来有 N 行，每行格式为：

1	`Address Data Next`

其中 Address 是结点地址，Data 是该结点保存的整数数据，Next 是下一结点的地址。

输出格式：

对每个测试用例，顺序输出反转后的链表，其上每个结点占一行，格式与输入相同。

输入样例：

00100 6 4
00000 4 99999
00100 1 12309
68237 6 -1
33218 3 00000
99999 5 68237
12309 2 33218

输出样例：

00000 4 33218
33218 3 12309
12309 2 00100
00100 1 99999
99999 5 68237
68237 6 -1

题解

思路

代码里写了注释，这里的代码参考网上的代码，自己瞎写的跑不出来......一个重要的思路是，把输入的address映射到具体数组的下标里。

代码

#include <stdlib.h>
#include <iostream>

using namespace std;

typedef struct
{
    int address; //节点地址
    int data;    //整数数据
    int next;    //下一节点的地址
} Node;

int main()
{
    int addr, N, K; //读取首地址，节点数量，反转个数
    scanf("%d %d %d", &addr, &N, &K);
    Node origin[100001], sort[100001]; //创建初始单链表,反转后的单链表
    for (int i = 0; i < N; i++)
    { //读取节点
        Node temp;
        scanf("%d %d %d", &temp.address, &temp.data, &temp.next);
        origin[temp.address] = temp;
    }

    for (int i = 0; i < N; i++)
    { //链接节点
        sort[i] = origin[addr];
        addr = sort[i].next; //获取下一个节点的地址
        if (addr == -1)
        {
            N = i + 1; //可能有无效的节点，需要更新链表中节点的数量
            break;
        }
    }

    for (int i = 0; i < N / K; i++)
    { //反转的次数
        for (int j = 0; j < K / 2; j++)
        { //反转
            Node temp;
            temp = sort[j + i * K];
            sort[j + i * K] = sort[K - 1 - j + i * K]; //数组下标确认好
            sort[K - 1 - j + i * K] = temp;
        }
    }

    for (int i = 0; i < N; i++)
    {
        if (i != N - 1)
        {
            sort[i].next = sort[i + 1].address;
            printf("%05d %d %05d\n", sort[i].address, sort[i].data, sort[i].next);
        }
        else
        {
            sort[i].next = -1;
            printf("%05d %d %d\n", sort[i].address, sort[i].data, sort[i].next);
        }
    }

    system("pause");
    return 0;
}

printf()函数可以控制格式输出，尤其在输出00010这种数据非常便捷：

printf("%05d", 10); // 输出五位正整数，不足五位用 0 补齐。

1026 程序运行时间 (15 分)

题目

要获得一个 C 语言程序的运行时间，常用的方法是调用头文件 time.h，其中提供了 clock() 函数，可以捕捉从程序开始运行到 clock() 被调用时所耗费的时间。这个时间单位是 clock tick，即“时钟打点”。同时还有一个常数 CLK_TCK，给出了机器时钟每秒所走的时钟打点数。于是为了获得一个函数 f 的运行时间，我们只要在调用 f 之前先调用 clock()，获得一个时钟打点数 C1；在 f 执行完成后再调用 clock()，获得另一个时钟打点数 C2；两次获得的时钟打点数之差 (C2-C1) 就是 f 运行所消耗的时钟打点数，再除以常数 CLK_TCK，就得到了以秒为单位的运行时间。

这里不妨简单假设常数 CLK_TCK 为 100。现给定被测函数前后两次获得的时钟打点数，请你给出被测函数运行的时间。

输入格式：

输入在一行中顺序给出 2 个整数 C1 和 C2。注意两次获得的时钟打点数肯定不相同，即 C1 < C2，并且取值在 [0,107]。

输出格式：

在一行中输出被测函数运行的时间。运行时间必须按照 hh:mm:ss（即2位的 时:分:秒）格式输出；不足 1 秒的时间四舍五入到秒。

输入样例：

1	`123 4577973`

输出样例：

1	`12:42:59`

题解：

思路

其实很简单，首先C2-C1然后四舍五入，然后再计算就好，记得按hh:mm:ss格式输出。

代码

#include <iostream>

using namespace std;

int main()
{
    long long c1, c2, run;

    cin >> c1 >> c2;

    run = ((c2 - c1) / 100.0 - (c2 - c1) / 100) >= 0.5 ? (c2 - c1) / 100 + 1 : (c2 - c1) / 100;

    printf("%02d:%02d:%02d", run / 3600, run / 60 % 60, run % 60);

    system("pause");
    return 0;
}

1027 打印沙漏（20分）

题目

本题要求你写个程序把给定的符号打印成沙漏的形状。例如给定17个“*”，要求按下列格式打印

*****
 ***
  *
 ***
*****

所谓“沙漏形状”，是指每行输出奇数个符号；各行符号中心对齐；相邻两行符号数差2；符号数先从大到小顺序递减到1，再从小到大顺序递增；首尾符号数相等。

给定任意N个符号，不一定能正好组成一个沙漏。要求打印出的沙漏能用掉尽可能多的符号。

输入格式:

输入在一行给出1个正整数N（≤1000）和一个符号，中间以空格分隔。

输出格式:

首先打印出由给定符号组成的最大的沙漏形状，最后在一行中输出剩下没用掉的符号数。

输入样例:

19 *

输出样例:

*****
 ***
  *
 ***
*****
2

题解

思路

这道题目本质上应该是一个数学题，把中间的设置为 1 的话，从中间往上就是 1，2，3......；从中间往下也是1，2，3......；但是去重之后，往下应该是2，3......。

每行对应的关系：

根据这个写代码就可以了。

代码

#include <iostream>

using namespace std;

int main()
{
    long long b;
    string s;
    cin >> b >> s;

    long long x = 1;

    while (2 * x * x - 1 < b)
    {
        x++;
    }
    if (x != 1)
    {
        x--;
    }

    for (long long i = x; i > 0; i--)
    {
        for (long long j = 0; j < x - i; j++)
        {
            cout << ' ';
        }
        for (long long j = (x - i) * 2; j < 2 * x - 1; j++)
        {
            cout << s;
        }
        cout << endl;
    }
    for (long long i = 2; i <= x; i++)
    {
        for (long long j = 0; j < x -i; j++)
        {
            cout << " ";
        }
        for (long long j = 0; j < 2 * i - 1; j++)
        {
            cout << s;
        }
        cout << endl;
    }
    cout << b - (2 * x * x - 1);

    system("pause");
    return 0;
}

1028 人口普查 (20 分)

题目

某城镇进行人口普查，得到了全体居民的生日。现请你写个程序，找出镇上最年长和最年轻的人。

这里确保每个输入的日期都是合法的，但不一定是合理的——假设已知镇上没有超过 200 岁的老人，而今天是 2014 年 9 月 6 日，所以超过 200 岁的生日和未出生的生日都是不合理的，应该被过滤掉。

输入格式：

输入在第一行给出正整数 N，取值在(0,105]；随后 N 行，每行给出 1 个人的姓名（由不超过 5 个英文字母组成的字符串）、以及按 yyyy/mm/dd（即年/月/日）格式给出的生日。题目保证最年长和最年轻的人没有并列。

输出格式：

在一行中顺序输出有效生日的个数、最年长人和最年轻人的姓名，其间以空格分隔。

输入样例：

5
John 2001/05/12
Tom 1814/09/06
Ann 2121/01/30
James 1814/09/05
Steve 1967/11/20

输出样例：

1	`3 Tom John`

题解

思路

出生日期格式已经固定，所以直接比较即可。

代码

#include <iostream>

using namespace std;

int main()
{
    int n, cnt = 0;
    cin >> n;
    string name, birth, maxname, minname, maxbirth = "1814/09/06", minbirth = "2014/09/06";

    for (int i = 0; i < n; i++)
    {
        cin >> name >> birth;
        if (birth >= "1814/09/06" && birth <= "2014/09/06")
        {
            cnt++;
            if (birth >= maxbirth)
            {
                maxbirth = birth;
                maxname = name;
            }
            if (birth <= minbirth)
            {
                minbirth = birth;
                minname = name;
            }
        }
    }
    cout << cnt;
    if (cnt != 0)
        cout << " " << minname << " " << maxname;

    system("pause");
    return 0;
}

1029 旧键盘（20分）

题目

旧键盘上坏了几个键，于是在敲一段文字的时候，对应的字符就不会出现。现在给出应该输入的一段文字、以及实际被输入的文字，请你列出肯定坏掉的那些键。

输入格式：

输入在 2 行中分别给出应该输入的文字、以及实际被输入的文字。每段文字是不超过 80 个字符的串，由字母 A-Z（包括大、小写）、数字 0-9、以及下划线 _（代表空格）组成。题目保证 2 个字符串均非空。

输出格式：

按照发现顺序，在一行中输出坏掉的键。其中英文字母只输出大写，每个坏键只输出一次。题目保证至少有 1 个坏键。

输入样例：

1 2	`7_This_is_a_test _hs_s_a_es`

输出样例：

7TI

题解

思路

分析：考的是字符串相关的知识，很容易想到的一种做法是将第一个字符串s1的每个字符和s2的每个字符做比较，然后如果s2中没有对应的字符，就是坏掉的键。

手工比较当然可以，但是发现string已经有了这样的查找操作。find()

例如：s2.find('a')将查找字符'a'，并返回a第一次出现的位置。如果没有就返回string::npos。

参考：1029 旧键盘（20分）

代码

#include <iostream>
#include <string>
#include <cctype>

using namespace std;

int main()
{
    string s1, s2, ans;
    cin >> s1 >> s2;

    for (int i = 0; i < s1.length(); i++)
    {
        if (s2.find(s1[i]) == string::npos && ans.find(toupper(s1[i])) == string::npos)
            ans += toupper(s1[i]);
    }
    cout << ans;

    system("pause");
    return 0;
}

1030 完美数列（20分）

1031 查验身份证（15分）

题目

一个合法的身份证号码由17位地区、日期编号和顺序编号加1位校验码组成。校验码的计算规则如下：

首先对前17位数字加权求和，权重分配为：{7，9，10，5，8，4，2，1，6，3，7，9，10，5，8，4，2}；然后将计算的和对11取模得到值Z；最后按照以下关系对应Z值与校验码M的值：

1 2	`Z：0 1 2 3 4 5 6 7 8 9 10 M：1 0 X 9 8 7 6 5 4 3 2`

现在给定一些身份证号码，请你验证校验码的有效性，并输出有问题的号码。

输入格式：

输入第一行给出正整数N（≤100）是输入的身份证号码的个数。随后N行，每行给出1个18位身份证号码。

输出格式：

按照输入的顺序每行输出1个有问题的身份证号码。这里并不检验前17位是否合理，只检查前17位是否全为数字且最后1位校验码计算准确。如果所有号码都正常，则输出All passed。

输入样例1：

4
320124198808240056
12010X198901011234
110108196711301866
37070419881216001X

输出样例1：

1
2
3

12010X198901011234
110108196711301866
37070419881216001X

输入样例2：

1
2
3

2
320124198808240056
110108196711301862结尾无空行

输出样例2：

1	`All passed`

题解

思路

这道题目很简单，思路也比较清晰的。

初始化权重数组，M数组。加权求和，再求模，然后根据M的下标，对应校验码，如果对的上，计数加一，否则输出即可。

代码

#include <iostream>

using namespace std;

int main()
{
    int n;
    cin >> n;

    int wei[] = {7, 9, 10, 5, 8, 4, 2, 1, 6, 3, 7, 9, 10, 5, 8, 4, 2};
    char M[] = {'1', '0', 'X', '9', '8', '7', '6', '5', '4', '3', '2'};
    string *s = new string[n];
    for (int i = 0; i < n; i++)
    {
        cin >> s[i];
    }

    // 通过的数目
    int passN = 0;
    for (int i = 0; i < n; i++)
    {
        int len = s[i].length();
        int sumI = 0;
        for (int j = 0; j < len - 1; j++)
        {
            sumI += int(s[i][j] - 48) * wei[j];
        }

        int Z = sumI % 11;

        if (M[Z] == s[i][17])
        {
            passN++;
        }
        else
        {
            cout << s[i] << endl;
        }
    }
    if (passN == n)
    {
        cout << "All passed" << endl;
    }

    system("pause");
    return 0;
}

1032 挖掘机技术哪家强（20分）

题目

为了用事实说明挖掘机技术到底哪家强，PAT 组织了一场挖掘机技能大赛。现请你根据比赛结果统计出技术最强的那个学校。

输入格式：

输入在第 1 行给出不超过 105 的正整数 N，即参赛人数。随后 N 行，每行给出一位参赛者的信息和成绩，包括其所代表的学校的编号（从 1 开始连续编号）、及其比赛成绩（百分制），中间以空格分隔。

输出格式：

在一行中给出总得分最高的学校的编号、及其总分，中间以空格分隔。题目保证答案唯一，没有并列。

输入样例：

输出样例：

2 150

题解

思路

思路还是很清晰，因为键值唯一，所以考虑字典，C++中字典为Map。具体看代码，写的还是比较清晰的。

代码

#include <iostream>
// #include <vector>
#include <map>

using namespace std;

int main()
{
    long num = 0;

    cin >> num;

    map<long, long long> m;
    for (long i = 0; i < num; i++)
    {
        long sch = 0;
        long long sco = 0;
        cin >> sch >> sco;
        if (m.count(sch) > 0)
        {
            sco += m[sch];
            m[sch] = sco;
        }
        else
        {
            // 
            m.insert(pair<long, long long>(sch, sco));
        }
    }

    map<long, long long>::iterator iter;
    long maxSch = 0;
    long long maxSco = INT16_MIN;
    for (iter = m.begin(); iter != m.end(); iter++)
    {
        if (iter->second > maxSco)
        {
            maxSco = iter->second;
            maxSch = iter->first;
        }
    }
    cout << maxSch << " " << maxSco << endl;

    system("pause");
    return 0;
}

1033 旧键盘打字 (20 分)

题目

旧键盘上坏了几个键，于是在敲一段文字的时候，对应的字符就不会出现。现在给出应该输入的一段文字、以及坏掉的那些键，打出的结果文字会是怎样？

输入格式：

输入在 2 行中分别给出坏掉的那些键、以及应该输入的文字。其中对应英文字母的坏键以大写给出；每段文字是不超过 105 个字符的串。可用的字符包括字母 [a-z, A-Z]、数字 0-9、以及下划线 _（代表空格）、,、.、-、+（代表上档键）。题目保证第 2 行输入的文字串非空。

注意：如果上档键坏掉了，那么大写的英文字母无法被打出。

输出格式：

在一行中输出能够被打出的结果文字。如果没有一个字符能被打出，则输出空行。

输入样例：

1 2	`7+IE. 7_This_is_a_test.`

输出样例：

1	`_hs_s_a_tst`

题解

思路

思路还是很朴素的，每种情况分别讨论。需要注意的是要使用getline()函数，否则第三个测试点不通过，因为字符串一为空。

代码

#include <iostream>

using namespace std;

int main()
{
    string broke, input;

    getline(cin, broke);
    getline(cin, input);

    int count = input.length();
    int len_b = broke.length();
    bool shift = true;

    // // find()函数：找到了返回起始位置；没找到返回npos。
    // // 如果没找到大写可用；如果找到了大写不可用。
    // if (broke.find('+') == broke.npos)
    // {
    //     shift = false;
    // }

    for (int i = 0; i < len_b; i++)
    {
        if (broke[i] == '+')
        {
            shift = false;
        }
        else if (broke[i] >= 'A' && broke[i] <= 'Z')
        {
            broke[i] += 32;
        }
    }

    string res = "";
    // 遍历查找不能用的键
    for (int i = 0; i < count; i++)
    {

        // 如果是大写字母，大写键不坏，字母键不坏
        if ((input[i] >= 'A' && input[i] <= 'Z') && shift && (broke.find(char(input[i] + 32)) == broke.npos))
        {
            res += input[i];
        }
        // 小写字母键不坏
        else if (input[i] >= 'a' && input[i] <= 'z' && broke.find(input[i]) == broke.npos)
        {
            res += input[i];
        }
        else if (!(input[i] >= 'A' && input[i] <= 'Z'))
        {
            int j = 0;
            for (; j < len_b; j++)
            {
                if (input[i] == broke[j])
                {
                    break;
                }
            }
            if (j >= len_b)
            {
                res += input[i];
            }
        }
    }

    cout << res << endl;

    system("pause");
    return 0;
}

1034 有理数四则运算 (20 分)

题目

本题要求编写程序，计算 2 个有理数的和、差、积、商。

输入格式：

输入在一行中按照 a1/b1 a2/b2 的格式给出两个分数形式的有理数，其中分子和分母全是整型范围内的整数，负号只可能出现在分子前，分母不为 0。

输出格式：

分别在 4 行中按照 有理数1 运算符有理数2 = 结果 的格式顺序输出 2 个有理数的和、差、积、商。注意输出的每个有理数必须是该有理数的最简形式 k a/b，其中 k 是整数部分，a/b 是最简分数部分；若为负数，则须加括号；若除法分母为 0，则输出 Inf。题目保证正确的输出中没有超过整型范围的整数。

输入样例 1：

1	`2/3 -4/2`

输出样例 1：

2/3 + (-2) = (-1 1/3)
2/3 - (-2) = 2 2/3
2/3 * (-2) = (-1 1/3)
2/3 / (-2) = (-1/3)

输入样例 2：

5/3 0/6

输出样例 2：

1 2/3 + 0 = 1 2/3
1 2/3 - 0 = 1 2/3
1 2/3 * 0 = 0
1 2/3 / 0 = Inf

题解

思路

分数的计算公示如下所示： \[ \begin{align} &\frac{a_1}{b_1} + \frac{a_1}{b_1} = \frac{a_1b_2 +a_2b_1}{b_1b_2} \\ &\frac{a_1}{b_1} - \frac{a_1}{b_1} = \frac{a_1b_2 - a_2b_1}{b_1b_2} \\ &\frac{a_1}{b_1} × \frac{a_1}{b_1} = \frac{a_1a_2}{b_1b_2} \\ &\frac{a_1}{b_1} ÷ \frac{a_1}{b_1} = \frac{a_1b_2}{a_2b_1} \end{align} \] 分数的化简需要辗转相除法（代码中为gcd()）。同时需要根据符号控制格式输出，如果异号，也要注意输出符号之前把数字绝对值化。代码为柳神的代码，向柳神学习呀，根据自己的理解写了一些注释。

代码

#include <iostream>
#include <cmath>

using namespace std;

long long a, b, c, d;

// 计算最大公约数，辗转相除法
long long gcd(long long t1, long long t2)
{
    return t2 == 0 ? t1 : gcd(t2, t1 % t2);
}

void func(long long m, long long n)
{
    // 分子分母出现0的情况，根据具体位置输出Inf与0
    if (m * n == 0)
    {
        printf("%s", n == 0 ? "Inf" : "0");
        return;
    }
    // 异号的情况
    bool flag = ((m < 0 && n > 0) || (m > 0 && n < 0));
    m = abs(m);
    n = abs(n);
    // x的值为分数约分得到的整数
    long long x = m / n;
    // 根据flag确定符号
    printf("%s", flag ? "(-" : "");
    // x不为零就输出，为0不输出
    if (x != 0)
        printf("%lld", x);
    // 如果余数为0，已经最简了，输出之后return即可
    if (m % n == 0)
    {
        if (flag)
            printf(")");
        return;
    }
    // 不是最简要继续，x不为0要输出一个空格
    if (x != 0)
        printf(" ");
    // 得到余数
    m = m - x * n;
    // 求最简分数
    long long t = gcd(m, n);
    m = m / t;
    n = n / t;
    printf("%lld/%lld%s", m, n, flag ? ")" : "");
}

int main()
{
    scanf("%lld/%lld %lld/%lld", &a, &b, &c, &d);
    func(a, b);
    printf(" + ");
    func(c, d);
    printf(" = ");
    func(a * d + b * c, b * d);
    printf("\n");
    func(a, b);
    printf(" - ");
    func(c, d);
    printf(" = ");
    func(a * d - b * c, b * d);
    printf("\n");
    func(a, b);
    printf(" * ");
    func(c, d);
    printf(" = ");
    func(a * c, b * d);
    printf("\n");
    func(a, b);
    printf(" / ");
    func(c, d);
    printf(" = ");
    func(a * d, b * c);

    system("pause");
    return 0;
}

#PAT

PAT乙级备考

https://excelius.xyz/pat乙级备考/

作者

Ther

发布于

2021年4月30日

许可协议

机器学习入门上一篇

LeetCode 633.平方数之和下一篇